Combinatorial lower bounds for the Generalized Traveling Salesman Problem with Neighborhoods
Authors: Deckerová, Jindřiška and Váňa, Petr and Faigl, Jan
Link: https://www.sciencedirect.com/science/article/pii/S0957417424020529?via%3Dihub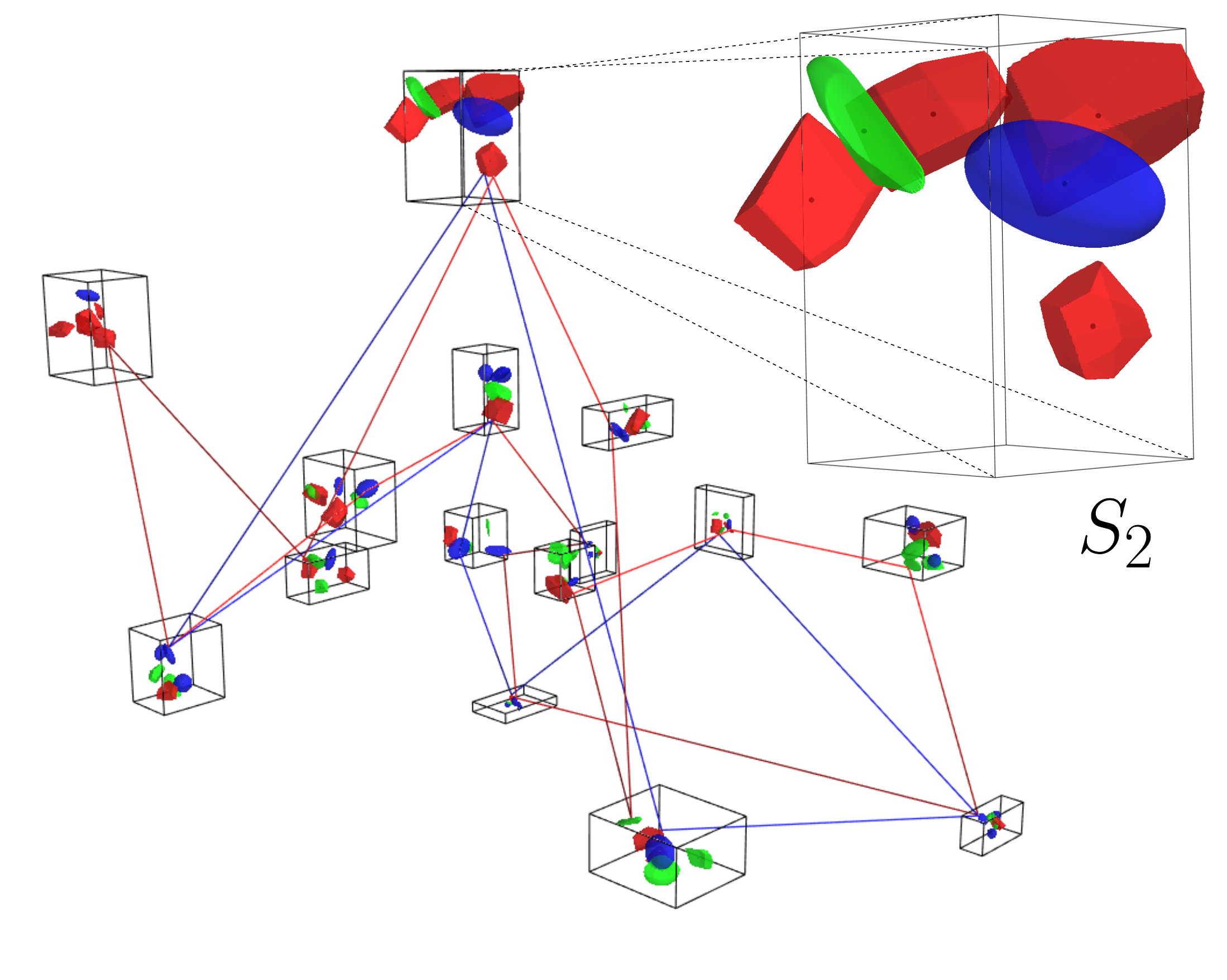
The Generalized Traveling Salesman Problem wing Neighborhoods (GTSPN) is solver with the Branch-and-Bound (B&B) method that uses Mixed-Integer Second-Order Cone Programming (MISOCP) to formulate the complex problem.
Abstract
In this paper, we study the Generalized Traveling Salesman Problem with Neighborhoods (GTSPN), a variant of the Traveling Salesman Problem (TSP), where the goal is to find the shortest path visiting each of the given neighborhood sets represented as a set of convex regions. The GTSPN is motivated by the sequencing problem of robotic manipulators, where an operation can be achieved from multiple locations, such as the visual inspection that can be performed from several possible views. The GTSPN formulation allows for exploiting continuous optimization to find the most suitable locations for the inspection, yielding possible solution cost reduction. Moreover, instances with overlapping high-dimensional convex regions further allow modeling neighborhood sets with complex shapes. We propose a novel approach to determine the first lower bounds to the studied GTSPN by employing the Branch-and-Bound (BB) method and the Mixed-Integer Second-Order Cone Programming (MISOCP) model for particular BB subproblems. In addition, the proposed method allows for solving the GTSPN to optima. The developed lower bound determination is further exploited in the empirical evaluation of existing heuristic approaches to the GTSPN and assesses the solution quality using the relative optimality gap. Regarding the presented results, the proposed BB-based approach provides tight lower bounds and solutions with up to 20 % optimality gap for the GTSPN instances with less than 15 neighborhood sets for the given limited computational time. Furthermore, the presented results support that the proposed approach is suitable for solving high-dimensional instances of the GTSPN that can be found in inspection tasks with robotic manipulators.Citation
author = {Deckerová, Jindřiška and Váňa, Petr and Faigl, Jan},
title = {Combinatorial lower bounds for the Generalized Traveling Salesman Problem with Neighborhoods},
journal= {Expert Systems with Applications},
volume= {258},
number= {},
pages = {125185},
year = {2024},
doi = {https://doi.org/10.1016/j.eswa.2024.125185},
}

Jindřiška Deckerová
I am 4th year PhD student at the Czech Technical University in Prague. I work in the Computational Robotics Laboratory with the Articial Inteligence Center in Faculty of Electrical Engineering. My main focus is on the routing problems, the optimal solution of these problems and solution in dynamic environments. Besides, one of my hobbies is popularization of science.
I have a podcast with my friend Míša called věda bez cenzury where we talk about doctorate studies, academia, and science.


